PSEB 8th Class Maths Solutions Chapter 4 Practical Geometry Ex 4.2

by

Punjab State Board PSEB 8th Class Maths Book Solutions Chapter 4 Practical Geometry Ex 4.2 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 8 Maths Chapter 4 Practical Geometry Ex 4.2

1. Construct the following quadrilaterals:

Question (i).
Quadrilateral LIFT.
LI = 4 cm,
IF = 3 cm,
TL = 2.5 cm,
LF = 4.5 cm,
IT = 4 cm.
Solution:
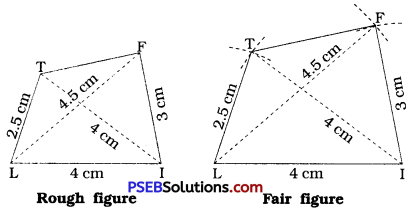
PSEB 8th Class Maths Solutions Chapter 4 Practical Geometry Ex 4.2 1

Steps of construction:

  • Draw a line segment LI = 4 cm.
  • With L as centre and radius = 2.5 cm, draw an arc.
  • With I as centre and radius = 4 cm, draw an arc to intersect the previous arc at T.
  • With L as centre and radius = 4.5 cm draw an arc.
  • With I as centre and radius 3 cm, draw an arc to intersect the previous, arc at F.
  • Draw \(\overline{\mathrm{LT}}, \overline{\mathrm{IF}}, \overline{\mathrm{FT}}, \overline{\mathrm{LF}}\) and \(\overline{\mathrm{IT}}\).

Thus, LIFT is the required quadrilateral.

Question (ii).
Quadrilateral GOLD
OL = 7.5 cm,
GL = 6 cm,
GD = 6 cm,
LD = 5 cm,
OD = 10 cm.
Solution:
PSEB 8th Class Maths Solutions Chapter 4 Practical Geometry Ex 4.2 2
Steps of construction:

  • Draw a line segment LD = 5 cm.
  • With L as centre and radius = 7.5 cm, draw an arc.
  • With D as centre and radius = 10 cm, draw another arc to intersect the previous arc at O.
  • With L as centre and radius = 6 cm, draw an arc.
  • With D as centre and radius = 6 cm, draw another arc to intersect previous arc at G.
  • Draw \(\overline{\mathrm{LO}}, \overline{\mathrm{GO}}, \overline{\mathrm{DG}}, \overline{\mathrm{LG}}\) and \(\overline{\mathrm{DO}}\).

Thus, GOLD is the required quadrilateral.

Question (iii).
Rhombus BEND
BN = 5.6 cm,
DE = 6.5 cm.
Solution:
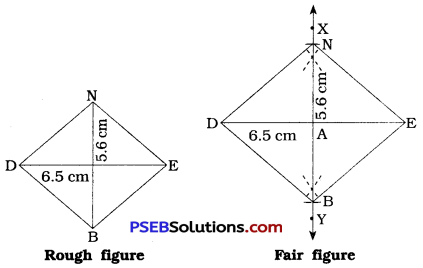
PSEB 8th Class Maths Solutions Chapter 4 Practical Geometry Ex 4.2 3a
[Note: Diagonals of a rhombus are perpendicular bisectors of each another. Here, diagonals of □ BEND \(\overline{\mathrm{DE}}\) and \(\overline{\mathrm{BN}}\) intersect at A. So AN = 2.8 cm and AB = 2.8 cm (BN = 5.6 cm, \(\frac {1}{2}\) BN = AN and AB)]
Steps of construction:

  • Draw a line segment DE = 6.5 cm.
  • Draw perpendicular bisector \(\overleftrightarrow{X Y}\) of \(\overline{\mathrm{DE}}\), which intersects \(\overline{\mathrm{DE}}\) at A.
  • With centre at A and radius = 5.6 × \(\frac {1}{2}\) = 2.8 cm, draw two arcs intersecting \(\overleftrightarrow{X Y}\) in points B and N.
  • Draw \(\overline{\mathrm{DN}}, \overline{\mathrm{EN}}, \overline{\mathrm{EB}}\) and \(\overline{\mathrm{DB}}\).

Thus, BEND is the required quadrilateral.

Leave a Comment