Punjab State Board PSEB 8th Class Maths Book Solutions Chapter 16 Playing with Numbers Ex 16.1 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 8 Maths Chapter 16 Playing with Numbers Ex 16.1
Find the values of the letters in each of the following and give reasons for the steps involved:
Question 1.

Solution:
Here, we have two letters A and B, whose values are to be found.

By observing the ones column, we have A + 5 and we get 2 from this.
1. e., a number whose ones digit is 2, for this A has to be 7.
∴ A + 5 = 7 + 5 = 12
Now, for the sum in tens column, we have 1 + 3 + 2 = B
∴ B = 6
Thus,

Thus, A = 7 and B = 6
![]()
Question 2.

Solution:
Here, we have three letters A, B and C, whose values are to be found.

By observing the ones column, we have A + 8 and we get 3 from this.
i. e., a number whose ones digit is 3, for this A has to be 5.
∴ A + 8 = 5 + 8 = 13
Now, for the sum in tens column, we have 1 + 4 + 9 = CB
∴ CB = 14
Here, B = 4 and C = 1

Thus, A = 5, B = 4 and C = 1
Question 3.
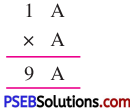
Solution:
Here, we have A, whose value is to be found.

Since, product of ones digit
A × A = A, so it must be 1, 5 or 6.
When A = 1, then 1 1 But, the product is 9 A, so A = 1 is not possible.

When A = 5, then
But, the product is 9 A, so A = 5 is not possible.

When A = 6, then

Thus, A = 6
![]()
Question 4.

Solution:
Here, we have two letters A and B, whose values are to be found.

By observing the ones column, we have B + 7 and we get A from this, i. e., a number whose ones digit is A.
Now, for the sum in tens column, we have A + 3 and we get 6 from this. Therefore, the value of A must be 2. (Keeping in mind that carry over 1 is to be considered.)
If A = 2, then

Then B + 7 gives 2, so B + 37 must be 5 and sum in tens 6 2 column is 1 + 2 + 3 = 6, so it is correct.

Question 5.

Solution:
Here, we have three letters A, B and C, whose values are to be found.

Units digit of 3 × B is B, so B must be either 0 or 5.
When B = 0, then

When B = 5, then

Now, units digit of 3 × A is A. So A must be either 0 or 5, but A cannot be 0, because if A = 0, then AB becomes one-digit number. So A must be 5 and multiplication is either 55 × 3 or 50 × 3.
55 × 3 = 165, here A = 6, so this is not possible.
∴ 50 × 3 = 150

Thus, A = 5, B = 0 and C = 6
![]()
Question 6.

Solution:
Here, we have three letters A, B and C, whose values are to be found.

Units digit B × 5 = B, so B must be either 0 or 5.
When B = 0, then

When B = 5, then

Now, units digit of 5 × A = A, so A must be either 0 or 5.
There are three letters as a product. So A ≠ 0, but A = 5.
So multiplication is either 50 × 5 or 55 × 5.
50 × 5 = 250 and 55 × 5 = 275, so 55 × 5 is not correct.
So 50 × 5 = 250

Thus, A = 5, B = 0 and C = 2.
![]()
Question 7.

Solution:
Here, we have two letters A and B, whose values are to be found.

Units digit B × 6 = B, so B must be 2, 4, 6 or 8.
∴ Possible values of product BBB are 222, 444, 666 or 888.
If we divide these numbers by 6, then quotient should be A2, A4, A6 or A8.
Now, 222 ÷ 6 = 37, remainder = 0
But, the quotient is not as A2, so B = 2 is not possible.

Thus, A = 7 and B = 4
Question 8.

Solution:
Here, we have two letters A and B, whose values are to be found.

By observing the sum in unit column, we have 1 + B = 0. So here is a number whose unit digit is 0, so B must be 9.
Now, for sum in tens column, we have 1 + A + 1 = 9.
So A must be 7.

Thus, A = 7 and B = 9
![]()
Question 9.

Solution:
Here, we have two letters A and B, whose values are to be found.

By observing the sum in units column, we have B + 1 = 8.
∴ B must be 7.
Now,

By observing the sum in tens digit column, we have A + 7 = 1, i.e., whose unit’s digit is 1, so A must be 4.

Thus, A = 4 and B = 7
![]()
Question 10.

Solution:
Here, we have two letters A and B, whose values are to be found.

By observing the sum in tens column, we have 2 + A = 0, so A must be 8.
Then,

Now, by observing the sum in units column, we have 8 + B = 9, so B must be 1.

Thus, A = 8 and B = 1.