PSEB 8th Class Maths Solutions Chapter 12 Exponents and Powers Ex 12.1

Punjab State Board PSEB 8th Class Maths Book Solutions Chapter 12 Exponents and Powers Ex 12.1 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 8 Maths Chapter 12 Exponents and Powers Ex 12.1

1. Evaluate:

Question (i)
3^-2
Solution:
= \(\frac{1}{3^{2}}\)
= \(\frac{1}{3 \times 3}\)
= \(\frac {1}{9}\)

Question (ii)
(-4)^-2
Solution:
= \(\frac{1}{(-4)^{2}}\)
= \(\frac{1}{(-4) \times(-4)}\)
= \(\frac {1}{9}\)

Question (iii)
(\(\frac {1}{2}\))^-5
Solution:
= \(\frac{1}{2} \times \frac{1}{2} \times \frac{1}{2} \times \frac{1}{2} \times \frac{1}{2}\)
= \(\frac{1}{\frac{1}{32}}\)
= 32

2. Simplify and express the result in power notation with positive exponent:

Question (i)
(-4)⁵ ÷ (-4)⁸
Solution:
= (-4)^{5 – 8} (∵ a^m ÷ aⁿ = a^m-n)
= (-4)^{– 3}
= \(\frac{1}{(-4)^{3}}\)

Question (ii)
\(\left(\frac{1}{2^{3}}\right)\)²
Solution:
= \(\frac{(1)^{2}}{\left(2^{3}\right)^{2}}\) [∵ \(\left(\frac{a}{b}\right)^{m}=\frac{a^{m}}{b^{m}}\)]
= \(\frac{1}{2^{3 \times 2}}\) [∵ (a^m)ⁿ = a^mn
= \(\frac{1}{2^{6}}\)

Question (iii)
(-3)⁴ × (\(\frac {5}{3}\))⁴
Solution:
= [(-3) × \(\frac {5}{3}\)]⁴ [∵ a^m × b^m = (ab)^m]
= [(-1) × 5]⁴
= (-1)⁴ × 5⁴
= 1 × 5⁴
= 5⁴

Question (iv)
(3^-7 ÷ 3^-10) × 3^-5
Solution:
= (3^(-7)-(-10)) × 3^-5 (∵ a^m ÷ aⁿ = a^m-n)
= (3^-7+10 × 3^-5
= 3³ × 3^-5
= 3³ + (-5) (∵ a^m × aⁿ = a^m+n)
= 3^-2
= \(\frac{1}{3^{2}}\)

Question (v)
2^-3 × (-7)^-3
Solution:
= [2 × (-7)]^-3 [∵ a^m × b^m = (ab)^m
= (-14)^-3
= \(\frac{1}{(-14)^{3}}\)

3. Find the value of:

Question (i)
(3⁰ + 4^-1) × 2²
Solution:
= (1 + \(\frac {1}{4}\)) × 2²
= (\(1 \frac{1}{4}\)) × 2²
= (\(\frac {5}{4}\)) × 4
= 5

Question (ii)
(2^{– 1} × 4^-1) ÷ 2²
Solution:
= (\(\frac {1}{2}\) × \(\frac {1}{4}\)) ÷ \(\frac{1}{2^{2}}\)
= (\(\frac {1}{8}\)) ÷ \(\frac {1}{4}\)
= \(\frac {1}{8}\) × \(\frac {4}{1}\)
= \(\frac {1}{2}\)

Question (iii)
(\(\frac {1}{2}\))^{– 2} + (\(\frac {1}{3}\))^{– 2} + (\(\frac {1}{4}\))^{– 2}
Solution:
=\(\frac{1}{\left(\frac{1}{2}\right)^{2}}+\frac{1}{\left(\frac{1}{3}\right)^{2}}+\frac{1}{\left(\frac{1}{4}\right)^{2}}\)
= \(\frac{1}{\frac{1}{4}}+\frac{1}{\frac{1}{9}}+\frac{1}{\frac{1}{16}}\)
= 4 + 9 + 16
= 29

Question (iv)
(3^{– 1} + 4^{– 1} + 5^{– 1})⁰
Solution:
(3^-1 + 4^-1 + 5^-1)⁰
∴ [3^-1 + 4^-1 + 5^-1]⁰ = 1
[∵ a⁰ = 1]

Question (v)
\(\left\{\left(\frac{-2}{3}\right)^{-2}\right\}\)²
Solution:
= \(\left(\frac{-2}{3}\right)^{(-2) \times 2}\) [∵ (a^m)^m = a^mn]
= (\(\frac {-2}{3}\))^-4
= \(\frac{(-2)^{-4}}{(3)^{-4}}\) [∵ \(\left(\frac{a}{b}\right)^{m}=\frac{a^{m}}{b^{m}}\)]
= \(\frac{3^{4}}{(-2)^{4}}\)
= \(\frac{3 \times 3 \times 3 \times 3}{(-2) \times(-2) \times(-2) \times(-2)}\)
= \(\frac {81}{16}\)

4. Evaluate:

Question (i)
\(\frac{8^{-1} \times 5^{3}}{2^{-4}}\)
Solution:
= \(\frac{2^{4} \times 5^{3}}{8}\)
= \(\frac{2^{4} \times 5^{3}}{2^{3}}\)
= 2^4-3 × 5³
= 2 × 125
= 250

Question (ii)
(5^-1 × 2^-1) × 6^-1
Solution:
= (\(\frac {1}{5}\) × \(\frac {1}{2}\)) × \(\frac {1}{6}\)
= (\(\frac {1}{10}\)) × \(\frac {1}{6}\)
= \(\frac {1}{60}\)

Another method:
= 5^-1 × 2^-1 × 6^-1
= (5 × 2 × 6)^-1
= (60)^-1
= \(\frac {1}{60}\)

5. Find the value of m for which 5^m ÷ 5^-3 = 5⁵.
Solution:
∴ 5^m-(-3) = 5⁵.
∴ 5^{m + 3} = 5⁵
∴ m + 3 = 5 (∵ a^m = aⁿ then m = n)
∴ m = 5 – 3
∴ m = 2
Thus, value of m is 2.

6. Evaluate:

Question (i)
\(\left\{\left(\frac{1}{3}\right)^{-1}-\left(\frac{1}{4}\right)^{-1}\right\}^{-1}\)
Solution:
= {\(\frac{3}{1}-\frac{4}{1}\)}^-1 (∵ a^-m = \(\frac {1}{a^m}\))
= {3 – 4}^-1
= {-1}^-1
= \(\frac {1}{-1}\)
= -1

Question (ii)
(\(\frac {5}{8}\))^-7 × (\(\frac {8}{5}\))^-4
Solution:
(\(\frac {5}{8}\))^-7 × (\(\frac {5}{8}\))⁴
(∵ a^-m = \(\frac{1}{a^{m}}\))
= (\(\frac {5}{8}\))^-7+4 (∵ a^m × aⁿ = a^m+n)
= (\(\frac {5}{8}\))^-3
= (\(\frac {8}{5}\))³
= \(\frac{8 \times 8 \times 8}{5 \times 5 \times 5}\)
= \(\frac {512}{125}\)

7. Simplify:

Question (i)
\(\frac{25 \times t^{-4}}{5^{-3} \times 10 \times t^{-8}}\) (t ≠ 0)
Solution:

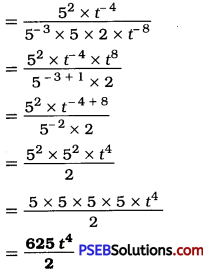
Question (ii)
\(\frac{3^{-5} \times 10^{-5} \times 125}{5^{-7} \times 6^{-5}}\)
Solution: