Punjab State Board PSEB 8th Class Maths Book Solutions Chapter 10 Visualising Solid Shapes InText Questions and Answers.
PSEB 8th Class Maths Solutions Chapter 10 Visualising Solid Shapes InText Questions
Do This : [Textbook Page No. 153 – 154]
1. Match the following: (First one is done for you.)
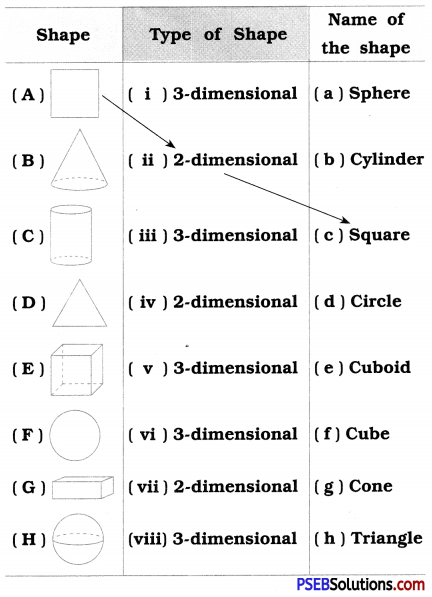
Solution:
(A) → (ii) → (c),
(B) → (iii) → (g),
(C) → (i) → (b),
(D) → (iv) → ( h ),
(E) → (v) → (f),
(F) → (vii) → (d),
(G) → (vi ) → (e),
(H) → (viii) → (a).
![]()
Do This : [Textbook Page No. 154 – 155]
1. Match the following pictures (objects) with their shapes:
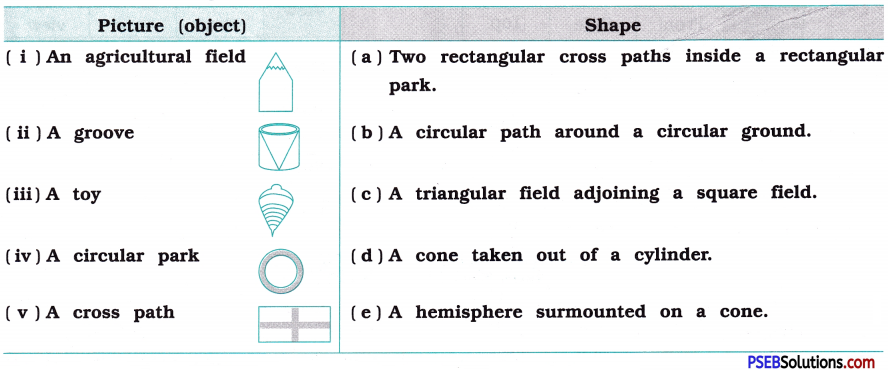
Solution:
(i) → (c),
(ii) → (d),
(iii) → (e),
(iv) → (b),
(v) → (a).
Do This : [Textbook Page No. 162-163]
1. Look at the following map of a city:
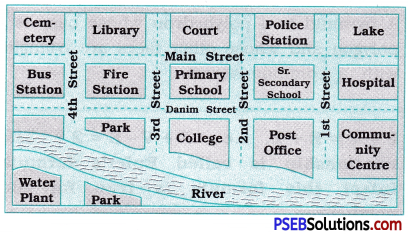
(a) Colour the map as follows: Blue – Water, Red – Fire Station, Orange – Library, Yellow – Schools, Green -Park, Pink – Community Centre, Purple – Hospital, Brown – Cemetery.
(b) Mark a Green ‘X’ at the intersection of 2nd street and Danim street. A Black ‘Y’ where the river meets the third street. A red ‘Z’ at the intersection of main street and 1st street.
(c) In magenta colour, draw a short street route from the college to the lake.
![]()
2. Draw a map of the route from your house to your school showing important landmarks.
[Note: Friends, do activity 1 and 2 by yourself. Enjoy drawing and colouring.]
Do This : [Textbook Page No. 165-166]
1. Tabulate the number of faces, edges and vertices for the following polyhedrons: (Here ‘V’ stands for number of vertices, ‘F’ stands for number of faces and ‘E’ stands for number of edges.)
| Solid | F | V | E | F + V | E + 2 |
| Cuboid | |||||
| Triangular pyramid | |||||
| Triangular prism | |||||
| Pyramid with square base | |||||
| Prism with square base |
What do you infer from the last two columns ? In each case, do you find F + V = E + 2, i.e., F + V – E = 2? This relationship is called Euler’s formula. Infact this formula is true for any polyhedron.
Solution:
| Solid | F | V | E | F + V | E + 2 |
| Cuboid | 6 | 8 | 12 | 6 + 8 =14 | 12 + 2 = 14 |
| Triangular pyramid | 4 | 4 | 6 | 4 + 4 = 8 | 6 + 2 = 8 |
| Triangular prism | 5 | 6 | 9 | 5 + 6 =11 | 9 + 2 =11 |
| Pyramid with square base | 5 | 5 | 8 | 5 + 5 = 10 | 8 + 2 = 10 |
| Prism with square base | 6 | 8 | 12 | 6 + 8 = 14 | 12 + 2 = 14 |
Yes, in each case Euler’s formula F + V = E + 2 or F + V – E = 2 is true.
Think, Discuss and Write : [Textbook Page No. 166]
1. What happens to F, V and E if some parts are sliced off from a solid ? (To start with, you may take a plasticine cube, cut a corner off and investigate.)
Solution:
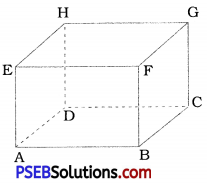
Suppose ABCDEFGH is a cube. It has 6 faces, 8 vertices and 12 edges.
V = 8, F = 6 and E = 12
∴ V + F – E
= 8 + 6 – 12 = 2
So the Euler’s formula is verified.
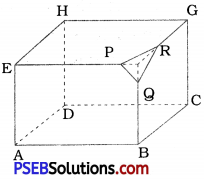
Now, suppose we sliced off ∆ PQR from this cube, then F = 6 + 1 = 7
V = 8 – 1 + 3
= 7 + 3 = 10
E = 12 + 3 = 15
∴ V + F – E = 10 + 7 – 15 = 2
∴ Here also Euler’s formula is verified. Thus, if some parts are sliced off a solid, then the number of vertices, edges and faces will be changed but still the Euler’s formula is verified.