Punjab State Board PSEB 12th Class Maths Book Solutions Chapter 1 Relations and Functions Ex 1.4 Textbook Exercise Questions and Answers.
PSEB Solutions for Class 12 Maths Chapter 1 Relations and Functions Ex 1.4
Question 1.
Determine whether or not each of the definition of * given below gives a binary operation. In the event that * is not a binary operation, give justification for this.
(i) On Z+, define * by a * b = a – b
(ii) On Z+, define * by a * b = ab
(iii) On R, define * by a * b = ab2
(iv) On Z+, define * by a * b = |a – b|
(v) On Z+, define * by a * b = a
Sol.
(i) On Z+, * is defined by a * b = a – b.
It is not a binary operation as the image of (1, 2) under * is
1 * 2 = 1 – 2 = – 1 ∉ Z+.
(ii) On Z+, * is defined by a * b = ab.
It is seen that for each a, b ∈ Z+, there is a unique element ab in Z+.
This means that * carries each pair (a, b) to a unique element a * b = ab in Z+. Therefore, * is a binary operation.
![]()
(iii) On R, * is defined by a * b = ab2.
It is seen that for each a, b ∈ R, there is a unique element ab2 in R.
This means that * carries each pair (a, b) to a unique element a * b = ab2 in R. Therefore, * is a binary operation.
(iv) On Z+, * is defined by a * b =|a – b|.
It is seen that for each a, b ∈ Z+, there is a unique element | a – b | in Z+. This means that * carries each pair (a, b) to a unique element a * b = |a – b|in Z+. Therefore, * is a binary operation.
(v) On Z+, * is defined by a * b = a.
It is seen that for each a, b ∈ Z+, there is a unique element a ∈ Z+. This means that * carries each pair (a, b) to a unique element a * b = a in Z+. Therefore, * is a binary operation.
![]()
Question 2.
For each operation * defined below, determine whether * is binary commutative or associative.
(i) On Z, define a* b = a – b
(ii) On Q, define a * b = ab + 1
(iii) On Q, define a* b = \(\frac{a b}{2}\)
(iv) On Z+, define a * b = 2ab
(v) On Z+, define a * b = ab
(vi) On R – {- 1},define a * b = \(\frac{a}{b+1}\)
Solution.
(i) On Z, operation * is defined as
(a) a * b = a – b
⇒ b * a = b – a
But a – b ≠ b – a
⇒ a * b ≠ b * a
∴ Defined operation is not commutative.
(b) a – (b – c) ≠ (a – b) – c
∴ Binary operation * as defined is not associative.
(ii) On Q, operation * is defined as a * b = ab +1
(a) ab + 1 = ba + 1, a * b = b * a
∴ Defined binary operation is commutative.
(b) a * (b * c) = a * (bc + 1) = a (bc + 1) + 1 = abc + a + 1
and (a * b)* c = (ab + 1) * c = (ab + 1)c + 1
= abc + c + 1
a * (b * c) ≠ (a * b) * c
∴ Binary operation defined is not associative.
(iii) (a) On Q, operation * is defined as a * b = \(\frac{ab}{2}\)
∴ a * b = b * a
∴ Operation binary defined is commutative.
(b) a * b = a * \(\frac{b c}{2}=\frac{a b c}{4}\)
and (a * b) * c = \(\frac{b c}{2}\) * c = \(\frac{a b c}{4}\)
⇒ Defined binary operation is associative.
![]()
(iv) On Z+, operation * is defined as a * b = 2ab
(a) a * b = 2ab, b * a = 2ba = 2ab
a * b = b * a
Binary operation defined is commutative.
(b) a * (b * c) = a * 2ba = 2a . bc
(a * b) * c = 2ab * c = 22ab
Thus, (a * b) * c ≠ a * (b * c)
∴ Binary operation * as defined is not associative.
(v) On Z+, a * b = ab
(a) b * a = ba
∴ ab = ba
⇒ a * b ≠ b * a
* is not commutative.
(b) (a * b) * c = ab * c
= (ab)c = abc
a * (b * c) = a * bc = abc.
This (a * b) * c ≠ (a * b * c)
∴ Operation * is not associative.
![]()
(vi) On Z+ operation * is defined as
a * b = \(\frac{a}{b+1}\), b ≠ – 1
∴ b * a = \(\frac{b}{a+1}\)
(a) a * b ≠ b * a
Binary operation defined is not commutative.
(b) (a * b) * c = \(a^{*}\left(\frac{b}{c+1}\right)=\frac{a}{\frac{b}{c+1}+1}=\frac{a(c+1)}{b+c+1}\)
(a * b) * c = \(\frac{a}{b+1} * c=\frac{\frac{a}{b+1}}{c+1}=\frac{a}{(b+1)(c+1)}\)
∴ a * (b * c) ≠ (a * b) * c
⇒ Binary operation defined above is not associative.
![]()
Question 3.
Consider the binary operation ^ on the set (1, 2, 3, 4, 5} defined by a ^ b = min {a, b}. Write the multiplication table of the operation ^.
Solution.
The binary operation ^ on the set {1, 2, 3, 4, 5} is defined as
a ^ b = min{a, b} for a, b ∈ {1, 2, 3, 4, 5}.
Thus, the operation table for the given operation ^ can be given as
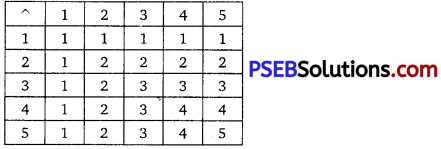
Question 4.
Consider a binary operation * on the set {1, 2, 3, 4, 5} given by the following multiplication table.
(i) Compute (2 * 3) * 4 and 2 * (3 * 4)
(ii) Is * commutative?
(iii) Compute (2* 3) * (4* 5).
(Hint: use the following table) (i)
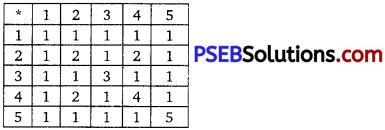
Solution.
(i) We have (2 * 3) *4 = 1 * 4 = 1
and 2 * (3 * 4) = 2 * 1 = 1
(ii) For every a, b ∈ (1, 2, 3, 4, 5}, we have a * b = b * a. Therefore, the operation * is commutative.
(iii) We have (2 * 3) = 1 and (4 * 5) = 1 .
∴ (2 * 3) * (4 * 5) = 1 * 1 = 1.
![]()
Question 5.
Let *’ be the binary operation on the set {1, 2, 3, 4, 5} is defined by a *’ b = H.C.F. of a and b. Is the operation *’ same as the operation * defined in Q. 4 above? Justify your answer.
Solution.
The binary operation *’ on the set {1, 2, 3, 4, 5} is defined as
a*’ b = HCF of a and b.
The operation table for the operation * can be given as :
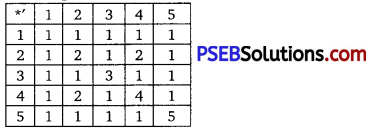
We observe that the operation table for the operations * and *’ are the same.
Thus, the operation *’ is same as the operation *.
Question 6.
Let * be the binary operation on N given by a * b = L.C.M. of a and b.
(i) Find 5 * 7, 20 * 16
(ii) Is * commutative?
(iii) Is * associative?
(iv) Find the identity of * in N.
(v) Which elements of N are invertible for the operation *?
Solution.
The binary operation * defined as a * b = L.C.M. of a and b
(i) 5 * 7 = L.C.M. of 5 and 7 = 35
and 20 * 16 = L.C.M. of 20 and 16 = 80
(ii) a * b = L.C.M. of a and b
b * a = L.C.M. of b and a
⇒ a * b = b * a L.C.M. of a, b and b, a are equal
∴ Binary operation * is commutative.
![]()
(iii) a * (b * c) = L.C.M. of a, b, c
and (a * b)* c = L.C.M. of a, b, c
⇒ a * (b * c) = (a * b) * c
⇒ Binary operation * is associative.
(iv) Identity of * in N is 1
1 * a = a * 1 = a = L.C.M. of 1 and a.
(v) Let * : N × N → N defined as a * b = L.C.M. of (a, b)
For a = 1, b = 1, a * b = 1 = b * a. Otherwise a * b ≠ 1
∴ Binary operation * is not invertible.
⇒ 1 is invertible for operaiton *.
Question 7.
Is * defined on the set {1, 2, 3, 4, 5} by a * 6 = L.C.M. of a and 6 a binary operation? Justify your answer.
Solution.
The operation * on the set A = {1, 2, 3, 4, 5} is defined as a * b = L.C.M. of a and b.
Now, 2 * 3 = L.C.M. of 2 and 3 = 6.
But 6 does not belong to the given set.
Hence, the given operation * is not a binary operation.
![]()
Question 8.
Let * be the binary operation on N defined by a * 6 = H.C.F. of a and b. Is * commutative? Is * associative? Does there exist identity for this binary operation on N?
Solution.
The binary operation * on N is defined as a * b = H.C.F. of a and b It is known that
H.C.F. of a and b = H.C.F. of b and a V a, b ∈ N.
∴ a * b = b * a
Thus, the operation * is commutative.
For a, b, c ∈ N, we have
(a * b) * c = (H.C.F. of a and b) * c = H.C.F. of a, b and c
a * (b * c) = a * (H.C.F. of b and c) = H.C.F. of a, b, and c
∴ (a * b) * c = a* (b * c)
Thus, the operation * is associative.
Now, an element e ∈ N will be the identity for the operation * if a * e = a = e * a for ∀ a ∈ N.
But this relation is not true for any a ∈ N.
Thus, the operation * does not have any identity in N.
![]()
Question 9.
Let * be a binary operation on the set Q of rational numbers as
(i) a * b = a – b
(ii) a * b = a2 + b2
(iii) a * b = a + ab
(iv) a * b = (a – b)2
(v) a * b = \(\frac{ab}{4}\)
(vi) a * b = ab2
Find which of the binary operations are commutative and which are associative.
Solution.
Operation is on the set Q.
(i) defined as a * b = a – b
(a) Now b * a = b – a But a – b *b – a
∴ a * b * b * a
∴ Operation * is not commutative.
(b) a* (b * c) = a * (b – c) = a – (b – c) = a – b + c
(a * b) * c = (a – b) * c = a – b – c
Thus, a * (b * c) ^ (a * b) * c
∴ The operation * as defined is not associative.
(ii) (a) a * b = a2 + b2
b * a = b2 + a2 = a2 + b2
∴ a * b = b * a
∴ This binary operation is commutative.
(b) a * (b * c) = a * (b2 + c2)
= a2 + (b2 + c2)2
(a * b) * c = (a2 + b2) * c = (a2 + b2)2 + c2
⇒ a * (b * c) * (a * b) * c
∴ The operation * given is not associative.
![]()
(iii) Operation * is defined as
a * b = a + ab
(a) b* a = b + ba
∴ a * b ≠ b * a
∴ This operation is not commutative.
(b) a * (b * c) = a * (b + bc)
= a + a(b + bc)
= a + ab + abc
(a* b) * c = (a + ab) *c = a + ab + (a + ab) . c
= a + ab + ac + abc
⇒ a* (b* c)& (a* b)* c
⇒ The binary operation is not associative.
(iv) The binary operation is defined as a * b = (a – b)2
(a) b * a = (b – a)2 = (a – b)2
⇒ a * b = b * a
∴ This binary operation * is commutative.
(b) a * (b * c) = a * (b – c)2
= [a – (b – c)2]2
(a * b) * c = (a – b)2 * c = [(a – b)2 – c]2
⇒ (a * b) * c ≠ a * (b * c)
Thus, the operation given is associative.
![]()
(v) Binary operation is * defined as
a * b = \(\frac{ab}{4}\)
(a) b * a = \(\frac{ba}{4}\) = \(\frac{ab}{4}\)
a* b^b* a
∴ The operation is not commutative.
(b) a * (b * c) = a * \(\frac{bc}{4}\)
= \(\frac{a}{4}\left(\frac{b c}{4}\right)=\frac{a b c}{16}\)
(a * b) * c = \(\frac{ab}{4}\) * c
= \(\frac{a b}{4} \cdot \frac{c}{4}=\frac{a b c}{16}\)
⇒ a * (b* c) = (a * b) * c
Thus, the operation given is associative.
![]()
(vi) Binary operation is defined as
a * b = ab2
(a) b * a = ba2 ≠ ab2
∴ a * b ≠ b * a
∴ The operation is not commutative.
(b) a * (b * c) = a * bc2
= a(bc2)2
= ab2c4
(a * b)* c = ab2 * c
= (ab2)c2
= ab2c2
∴ a * (b * c) ≠ (a * b) * c
∴ Binary operation * given is not associative.
![]()
Question 10.
Find which of the operations given above has identity.
Solution.
An element e ∈ Q will be the identity element for the operation * if
a * e = a = e * a, ∀ a ∈ Q
(i) a * b = a – b
lf a * e = a, a ≠ 0
⇒ a – e = a, a ≠ 0 ⇒ e = 0
Also, e * a = a
⇒ e – a = a ⇒ e = 2 a
e = 0 = 2a, a ≠ 0
But the identity is unique. Hence this operation has no identity.
(ii) a * b = a2 + b2
If a * e = a, then a2 + e2 = a
For a = – 2, (- 2)2 + e2 = 4 + e2 ≠ – 2
Hence, there is no identity element.
![]()
(iii) a * b = a + ab
If a * e = a
⇒ a + ae a
⇒ ae = 0
⇒ e = 0, a ≠ 0
Also a * e = a
⇒ e + ae = a
⇒ e = \(\frac{a}{a+1}\), a ≠ 1
∴ e = 0 = \(\frac{a}{a+1}\), a ≠ 0
But the identity in unique. Hence this operation has no identify.
(iv) a * b = (a – b)2
If a* e = a, then (a – e)2 = a.
A square is always positive, so for a = – 2, (- 2 – e)2 ≠ – 2.
Hence, there is no identity element.
(v) a * b – ab/ 4
If a * e = a, then ae / 4 = a.
Hence, e = 4 is the identity element.
∴ a * 4 = 4 * a = 4a/4 = a.
(vi) a * b = ab2
If a * e = a
⇒ ae2 = a
⇒ e2 = 1
⇒ e = ±1
But identity is unique. Hence this operation has no identity.
Therefore only part (v) has an identity element.
![]()
Question 11.
Let A = N × N and * be the binary operation on A defined by (a, b) * (c, d) = (a + c, b + d). Show that * is commutative and associative. Find the identity element for * on A, if any.
Solution.
Given that A = N × N and * is a binary operation on A and is defined by (a, b) * (c, d) = (a + c,b + d.)
Let (a, b), (c, d) ∈ A
Then, a, b, c, d ∈ N
We have (a, b) * (c, d) = (a + c, b + d)
and (c, d) * (a, b) = (c + a, d + b) = (a + c, b + d)
[Addition is commutative in the set of natural numbers]
∴ (a, b) * (c, d) = (c, d) * (a, b)
Therefore, the operation * is commutative.
Now, let (a, b), (c, d), (e, f) ∈ A
Then, a, b, c, d, e, f ∈ N
We have {(a, b) * (c, d)} * (e, f) = (a + c,b + d) * (e, f)
= (a+ c + e, b + d + f)
(a, b) * ((c, d) * (e, f)) = (a, b) * (c + e, d + f) = (a + c + e, b + d + f)
((a, b) * (c, d)) * (e, f) = (a, b) * ((c, d) * (e, f))
Therefore, the operation * is associative.
An element e = (e1, e2) ∈ A will be an identity element for the operation * if
a * e = a = e * a ∀ a = (a1, a2) ∈ A, i.e., (a1 + e1, a2 + e2)
= (a1, a2) = (e1 + a1; e2 + a2)
which is not true for any element in A.
Therefore, the operation * does not have any identity element.
![]()
Question 12.
State whether the following statements are true or false. Justify.
(i) For an arbitrary binaiy operation * on a set N, a * a = a ∀ a ∈ N.
(ii) If * is a commutative binary operation on N, then a* (b* c) = (c * b) * a
Solution.
(i) Define an operation * on IV as a * b – a + b ∀ a, b ∈ N
Then, in particular, for b = a = 3, we have 3 * 3 = 3 + 3 = 6 ≠ 3
Therefore, statement (i) is false.
(ii) R.H.S. = (c * b) * a
= (b * c) * a [* is commutative]
= a * (b * c) [Again, as * is commutative]
= L.H.S.
∴ a * (b * c) = (c * b) * a
Therefore, statement (ii) is true.
![]()
Question 13.
Consider a binary operation * on N defined as a * b = a3 +b3. Choose the correct answer.
(A) Is * both associative and commutative?
(B) Is * commutative but not associative?
(C) Is * associative but not commutative?
(D) Is * neither commutative nor associative?
Solution.
On N, the operation * is defined as a * b = a3 + b3.
For, a, b ∈ N, we have
a * b = a3 + b3
= b3 + a3 = b * a [Addition is commutative in N]
Therefore, the operation * is commutative.
It can be observed that
(1 * 2) * 3 = (13 + 23) * 3 = 9 * 3
= 93 + 33
= 729 + 27 = 756
1 * (2 * 3) = 1 * (23 +33)
= 1 * (8 + 27) = 1 * 35
= 13 + 353
= 1 + (35)3
= 1 + 42875 = 42876
∴ (1 * 2) * 3 ≠ 1 * (2 * 3) where 1, 2, 3 ∈ N
Therefore, the operation * is not associative.
Hence, the operation * is commutative, but not associative.
Thus, the correct answer is (B).