PSEB 12th Class Maths Solutions Chapter 1 Relations and Functions Ex 1.2

Punjab State Board PSEB 12th Class Maths Book Solutions Chapter 1 Relations and Functions Ex 1.2 Textbook Exercise Questions and Answers.

PSEB Solutions for Class 12 Maths Chapter 1 Relations and Functions Ex 1.2

Question 1.
Show that the function F: R → R, defined by f(x) = \(\frac{1}{x}\) is one-one and onto, where R, is the set of all non-zero real numbers. Is the result true, if the domain R. is replaced by N with co-domain being same as R?
Solution.
It is given that f: R. → R. is defined by f(x) = \(\frac{1}{x}\)
One-one :
f(x) = f(y)
⇒ \(\frac{1}{x}\) = \(\frac{1}{y}\)
⇒ x = y
∴ f is one-one.

Onto :
It is clear that for y ∈ R., there exists x = \(\frac{1}{y}\) ∈ R. (Exists as y ≠ 0) such that f(x) = \(\frac{1}{\left(\frac{1}{y}\right)}\) = y.
∴ f is onto.
Thus, the given function (f) is one-one and onto.
Now, consider function g :N →R, defined by
g(x) = \(\frac{1}{x}\)
We have,
g(x₁) = g(x₂)
⇒ \(\frac{1}{x_{1}}=\frac{1}{x_{2}}\)
x₁ = x₂
∴ g is one-one.
Further, it is clear that g is^not onto as for 1.2 ∈ R, there does not exist any x in N such that g(x) = \(\frac{1}{1.2}\).
Hence, function g is one-one but not onto.

Question 2.
Check the injectivity and surjectivity of the following functions
(i) f: N → N given by f(x) = x²
(ii) f: Z → Z given by f(x) = x²
(iii) f: R → R given by f(x) = x²
(vi) f: N → N given by f(x)) = x³
(v) f: Z → Z given by f(x) = x³
Solution.
(i) f: N → N is given by,
f(x) = x²
It is seen that for x, y ∈ N, f(x) = f(y)
⇒ x² = y²
⇒ x = y
∴ f is injective.
Now, 2 ∈ N. But, there does not exist any x in N such that f(x) = x² = 2.
∴ f is not surjective.
Hence, function f is injective but not surjective.

(ii) f: Z → Z is given by,
f(x) = x²
It is seen that f(- 1) = f(1) = 1, but = – 1 ≠ 1.
∴ f is not injective.
Now, – 2 ∈ Z. But, there does not exist any element x ∈ Z such that f(x) = x² = – 2
∴ f is not surjective.
Hence, function f is neither injective nor surjective.

(iii) f: R → R is given by, f(x) = x²
It is seen that f(- 1) = f(1) = 1, but -1 ≠ 1.
∴ f is not injective.
Now, – 2 ∈ R. But , there does not exist any element x ∈ R such that f(x) = x² = – 2.
∴ f is not surjective.
Hence, function f is neither injective nor surjective.

(iv) f : N → N given by,
f(x) = x³
It is seen that for x, y ∈ N, f(x) = f(y)
⇒ x³ = y³
⇒ x = y
∴ f is injective.
Now, 2 ∈ N. But, there does not exist any element x in domain N such that f(x) = x³ = 2.
∴ f is not surjective
Hence, function f is injective but not surjective.

(v) f: Z → Z is given by, f(x) = x3
It is seen that for x, y ∈ Z, f(x) = f(y)
⇒ x³ = y³
⇒ x = y.
∴ f is injective.
Now, 2 ∈ Z. But, there does not exist any element x in domain Z such that f(x) = x³ = 2.
∴ f is not surjective.
Hence, function f is injective but not surjective.

Question 3.
Prove that the greatest integer function f: R → R given by f(x) = [x], is neither one-one nor onto, where [x] denotes the greatest integer less than or equal to x.
Solution.
f: R → R is given by,
f(x) = [x]
It is seen that /(1.2) = [1.2] = 1,
f(1.9) = [1.9] = 1.
∴ f(1.2) = f(1.9), but 1.2 ≠ 1.9.
∴ f is not one-one.
Now, consider 0.7 ∈ R.
It is known that f(x) = [x] is always an integer. Thus, there does not exist any element x ∈ R such that f(x) = 0.7.
∴ f is not onto.
Hence, the greatest integer function is neither one-one nor onto.

Question 4.
Show that the modulus function f: R → R given by f(x) = |x|, is neither one-one nor onto, where x is x, if x is positive or 0 and |x| is – x, if x is negative.
Solution.
f: R → R is given by,
f(x) = |x| = {x, if x ≥ 0; – x if x < 0
It is seen that f(- 1) = |- 1| = 1, f(1) = |1| = 1.
∴ f(- 1) = f(1),but – 1 ≠ 1.
∴ f is not one-one.
Now, consider – 1 ∈ R.
It is known that f(x) = |x| is always non-negative,. Thus, there does not exist any element x in domain R such that f(x) = |x| = – 1.
∴ f is not onto.
Hence, the modulus function is neither one-one nor onto.

Question 5.
Show that the signum function f: R → R, given by

is neither one-one nor onto.
Solution.
f: R → R is given by,

It is seen that f(1) = f(2) = 1, but 1 ≠ 2.
∴ f is not one-one.
Now, as f(x) takes only 3 values (1, 0, or – 1) for the element – 2 in co-domain R, there does not exist any x in domain R such that f(x) = – 2.
∴ f is not onto.
Hence, the signum function is neither one-one nor onto.

Question 6.
Let A = {1, 2, 3,}, B = {4 5, 6, 7} and let f = {(1, 4), (2, 5), (3, 6)} be a function from A to B. Show that f is one-one.
Solution.
It is given that A = {1, 2, 3}, B = {4, 5, 6, 7}.
f: A → B is defined as f = {(1, 4), (2, 5), (3, 6)}.
∴ f(1) = 4, f(2) = 5, f(3) = 6
It is seen that the images of distinct elements of A under f are distinct. Hence, function f is one-one.

Question 7.
In each of the following cases, state whether the function is one-one, onto or bijective. Justify your answer.
(i) f: R → R defined as f(x) = 3 – 4x
(ii) f: R → R defined as f(x) = 1 + x³
Solution.
(i ) f: R → R is defined as f(x) = 3- 4x.
Let x₁, x₂ ∈ R such that f(x₁) = f(x₂)
⇒ 3 – 4x₁ = 3 – 4x₂
⇒ – 4x₁ = – 4x₁
⇒ x₁ = x₂
∴ f is one-one.
For any real number (y) in R, there exists \(\frac{3-y}{4}\) in R such that
f(\(\frac{3-y}{4}\)) = 3 – 4(\(\frac{3-y}{4}\)) = y
∴ f is onto.
Hence, f is bijective.

(ii) f: R → R is defined as f(x) = 1 + x²
Let x₁, x₂ ∈ R such that f(x₁) = f(x₂)
⇒ 1 + x₁² = 1 + x₂²
⇒ x₁² = ± x₂²
⇒ x₁ = x₂
⇒ f(x₁) = f(x₂) does not imply that x₁ = x₂.
For instance, f(1) = f(- 1) = 2
∴ f is not one-one.
Consider an element – 2 in co-domain R.
k is seen that f(x) = 1 + x² is positive for all x ∈ R.
Thus, there does not exist any x in domain R such that f(x) = – 2.
∴ f is not onto.
Hence, f is neither one-one nor onto.

Question 8.
Let A and B be sets. Show that f: A × B – B × A such that f (a, b) (b, a) is bijective function.
Solution.
f: A × B → B × A is defined as f(a, b) = (b, a).
Let(a₁, b₁), (a₂, b₂) ∈ A × B such that f(a₁, b₁) = f(a₂, b₂)
⇒ (b₁, a₁) = (b₂, a₂)
⇒ b₁ = b₂ and a₁ = a₂
⇒ (a₁, b₁) = (a₂, b₂)
∴ f is one – one.
Now, let (b, a) ∈ B × A be any element.
Then, there exists (a, b) ∈ A × B such that f(a, b) = (b, a). [by definition of f]
∴ f is onto.
Hence, f is bijective.

Question 9.
Let f: N → N be defined by

(n) =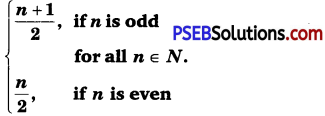

State whether the function is bijective. Justify your answer.
Solution.

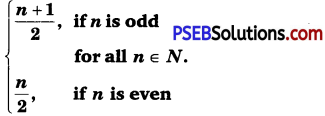
It can be observed that:
f(1) = \(\frac{1+1}{2}\) = 1 amnd f(2) = \(\frac{2}{2}\) = 1 [by definition of f]
∴ f(1) = f(2), where 1 ≠ 2.
∴ f is not one-one.
Consider a natural number (n) in co-domain N.

Case I: n is odd.
∴ n = 2r + 1 for some r ∈ N. Then, there exists 4r + 1 ∈ N such that
f(4r + 1) = \(\frac{4 r+1+1}{2}\) = 2r+ 1

Case II : n is even,
∴ n – 2r for some r ∈ N. Then there exists 4r ∈ N such that 4r
f(4r) = \(\frac{4r}{2}\) = 2r.
∴ f is onto.
Hence, f is not a bijective function.

Question 10.
Let A = R – {3} and B = R – {1}. Consider the function f: A → B defined by f(x) = \(\left(\frac{x-2}{x-3}\right)\). Is f one-one and onto? Justify your answer.
Solution.
Here, A = R – {3}, B = R – {1}
and f: A → B is defined as f(x) = \(\left(\frac{x-2}{x-3}\right)\)
Let x, y ∈ A such that f(x) = f(y).
⇒ \(\frac{x-2}{x-3}=\frac{y-2}{y-3}\)
⇒ (x – 2) (y – 3) = (y – 2) (x – 3)
⇒ xy – 3x – 2y + 6 = xy – 3y – 2x + 6
⇒ – 3x – 2y = – 3y – 2x
⇒ 3x – 2x = 3y – 2y
⇒ x = y
∴ f is one-one.
Let y ∈ B = R – {1}. Then, y ≠ 1.
The function f is onto if there exists x ∈ A such that f(x) = y.
Now, f(x) = y
⇒ \(\frac{x-2}{x-3}\) = y
⇒ x – 2 = xy – 3y
⇒ x(1 – y) = – 3y + 2
⇒ x = \(\frac{2-3 y}{1-y}\) ∈ A

Thus, for any y B, there exists \(\frac{2-3 y}{1-y}\) ∈ A such that
f(\(\frac{2-3 y}{1-y}\)) = \(\frac{\left(\frac{2-3 y}{1-y}\right)-2}{\left(\frac{2-3 y}{1-y}\right)-3}\)

= \(\frac{2-3 y-2+2 y}{2-3 y-3+3 y}=\frac{-y}{-1}\) = y

∴ f is onto.
Hence, function f is one-one and onto.

Question 11.
Let f: R → R be defined as f(x) = x⁴. Choose the correct answer.
(A) f is one-one onto
(B) f is many-one onto
(C) f is one-one but not onto
(D) f is neither one-one nor onto
Solution.
f : R → R is defined as f(x) = x4 Let x, yeR such that f(x) = f(y).
⇒ x⁴ = y⁴
⇒ x = ±y
∴ f(x₁) = f(x₂) does not imply that x₁ = x₂.
For instance,
f(1) = f(- 1) = 1
∴ f is not one-one.
Consider an element 2 in co-domain it. It is clear that there does not exist any x in domain R such that f(x) – 2 .
∴ f is not onto.
Hence, function f is neither one-one nor onto.
The correct answer is (D).

Question 12.
Let f: R → R be defined as f(x) = 3x. Choose the correct answer.
(A) f is one-one onto
(B) f is many-one onto
(C) f is one-one not onto
(D) f is neither one-one nor onto
Solution.
f: R → R is defined as f(x) = 3x.
Let x, y ∈ R such that f(x) = f(y).
⇒ 3x – 3y
⇒ x = y .
∴ f is one-one.
Also any real number (y) in co-domain R, there exists \(\frac{y}{3}\) in R such that
f(\(\frac{y}{3}\)) = 3(\(\frac{y}{3}\)) = y
∴ f is onto.
Hence, function f is one-one and onto.
The correct answer is (A).