Punjab State Board PSEB 8th Class Maths Book Solutions Chapter 1 Rational Numbers Ex 1.1Textbook Exercise Questions and Answers.
PSEB Solutions for Class 8 Maths Chapter 1 Rational Numbers Ex 1.1
1. Represent these numbers on the number line:
Question (i).
\(\frac {7}{4}\)
Solution:
To represent \(\frac {7}{4}\), make 7 markings each of a distance equal to \(\frac {1}{4}\) on the right side of 0. The 7th point represents the rational number \(\frac {7}{4}\).
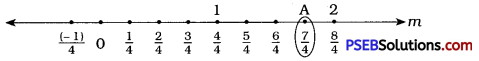
The point A is \(\frac {7}{4}\).
Question (ii).
\(\frac {-5}{6}\)
Solution:
To represent (\(\frac {-5}{6}\)) on the number line, make 5 markings each of a distance equal to on the left side of 0. The 5th point represents the rational number (\(\frac {-5}{6}\)).
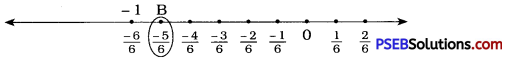
The point B is (\(\frac {-5}{6}\))
2. Represent \(\frac{-2}{11}, \frac{-5}{11}, \frac{-9}{11}\) on the number line.
Solution:
To represent the given rational numbers on a number line, make 11 markings each being equal to distance \(\frac {1}{11}\) on the left of 0.
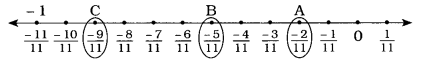
Here, the point A is (\(\frac {-2}{11}\)).
the point B is (\(\frac {-5}{11}\)).
the point C is (\(\frac {-9}{11}\)).
![]()
3. Write five rational numbers which are smaller than 2.
Solution:
There are infinite rational numbers below 2, positive as well as negative.
Five of them are 1, \(\frac {1}{3}\), \(\frac {1}{4}\), 0, – 1.
4. Find ten rational numbers between \(\frac {-2}{5}\) and \(\frac {1}{2}\).
Solution:
First, convert \(\frac {-2}{5}\) and \(\frac {1}{2}\) having the same denominator, such that the difference between the numerators is more than 10.
\(\frac{-2}{5}=\frac{-2}{5} \times \frac{4}{4}=\frac{-8}{20}\);
\(\frac{1}{2}=\frac{1}{2} \times \frac{10}{10}=\frac{10}{20}\)
∴ The ten rational numbers between \(\frac {-8}{20}\) and \(\frac {10}{20}\) are
\(\frac{-7}{20}, \frac{-6}{20}, \frac{-5}{20}, \frac{-4}{20}, \frac{-3}{20}, \ldots, 0, \frac{1}{20}, \ldots, \frac{9}{20} .\)
(There can be many more such rational numbers.)
5. Find five rational numbers between
Question (i).
\(\frac {2}{3}\) and \(\frac {4}{5}\)
Solution:
First, convert \(\frac {2}{3}\) and \(\frac {4}{5}\) having the same denominator, such that the difference between the numerators is more than 5.
\(\frac{2}{3}=\frac{2}{3} \times \frac{20}{20}=\frac{40}{60}\);
\(\frac{4}{5}=\frac{4}{5} \times \frac{12}{12}=\frac{48}{60}\)
∴ The five rational numbers between \(\frac {2}{3}\) and \(\frac {4}{5}\) are \(\frac{42}{60}, \frac{43}{60}, \frac{44}{60}, \frac{45}{60}, \frac{46}{60}\).
Question (ii).
\(\frac {-3}{2}\) and \(\frac {5}{3}\)
Solution:
First, convert \(\frac {-3}{2}\) and \(\frac {5}{3}\) having the same denominator, such that the difference between the numerators is more than 5.
\(\frac{-3}{2}=\frac{-3}{2} \times \frac{3}{3}=\frac{-9}{6}\);
\(\frac{5}{3}=\frac{5}{3} \times \frac{2}{2}=\frac{10}{6}\)
∴ The five rational numbers between \(\frac {-3}{2}\) and \(\frac {5}{3}\) are \(\frac{-8}{6}, \frac{-7}{6}, 0, \frac{7}{6}, \frac{8}{6}\).
Question (iii).
\(\frac {1}{4}\) and \(\frac {1}{2}\)
Solution:
First, convert \(\frac {1}{4}\) and \(\frac {1}{2}\) having the same denominator, such that the difference between the numerators is more than 5.
\(\frac{1}{4}=\frac{1}{4} \times \frac{8}{8}=\frac{8}{32}\);
\(\frac{1}{2}=\frac{1}{2} \times \frac{16}{16}=\frac{16}{32}\)
∴ The five rational numbers between \(\frac {1}{4}\) and \(\frac {1}{2}\) are \(\frac{10}{32}, \frac{11}{32}, \frac{12}{32}, \frac{13}{32}, \frac{14}{32}\).
(There can be many more such rational numbers.)
[Note : You can write rational numbers of your choice.]
![]()
6. Write five rational numbers greater than -2.
Solution:
There can be many rational numbers greater than – 2. Five of them are \(\frac{-3}{2}, \frac{-1}{4}, 0, \frac{1}{2}, \frac{1}{5}\).
7. Find ten rational numbers between \(\frac {3}{5}\) and \(\frac {3}{4}\).
Solution:
First, convert \(\frac {3}{5}\) and \(\frac {3}{4}\) having the same denominator, such that the difference between the numerators is more than 10.
\(\frac{3}{5}=\frac{3}{5} \times \frac{20}{20}=\frac{60}{100}\);
\(\frac{3}{4}=\frac{3}{4} \times \frac{25}{25}=\frac{75}{100}\)
∴ The ten rational numbers between \(\frac {3}{5}\) and \(\frac {3}{4}\) are \(\frac{61}{100}, \frac{62}{100}, \frac{63}{100}, \frac{64}{100}, \frac{65}{100}, \frac{66}{100}, \frac{67}{100}, \frac{68}{100},\)\(\frac{69}{100}, \frac{70}{100}\)